In our last post, we mentioned that the 'accuracy' statistic, also known as the probability of a correct result, was a useless measure for diagnostic test performance. Today we'll explain why.
Let's take a hypothetical test with a sensitivity of 86% and specificity of 98%.
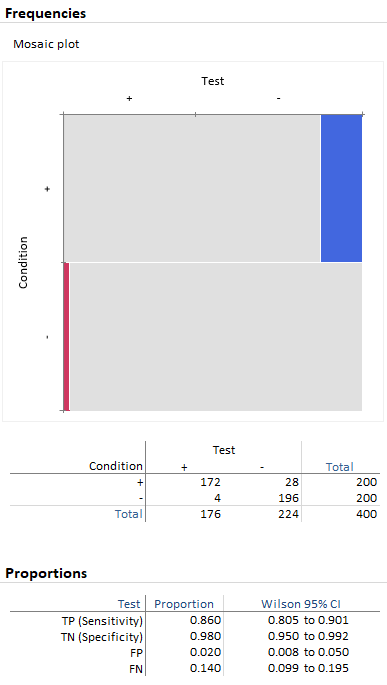
As a first scenario we simulated test results on 200 subjects with, and 200 without, the condition. The accuracy statistic (TP+TN)/N is equal to (172+196)/400 = 92%. See below:
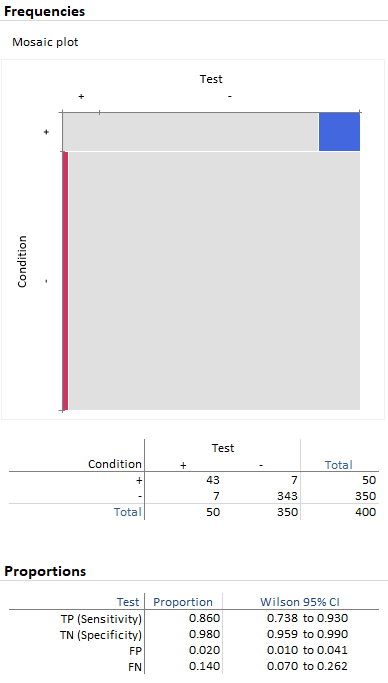
In a second scenario we again simulated test results on 400 subjects, but only 50 with, and 350 without, the condition. The accuracy statistic is (43+343)/400 = 96.5%. See below:
The accuracy statistic is effectively a weighted average of sensitivity and specificity, with weights equal to the sample prevalence P(D=1) and the complement of the prevalence (that is, P(D=0) = 1-P(D=1)).
Accuracy = P(TP or TN) = (TP+TN)/N = Sensitivity * P(D=1) + Specificity * P(D=0)
Therefore as the prevalence in the sample changes so does the statistic. The prevalence of the condition in the sample may vary due to the availability of subjects or it may be fixed during the design of the study. It's easy to see how to manipulate the accuracy statistic to weigh in favor of the measure that performs best.
Finally, the 'accuracy' statistic is not a good way of comparing diagnostic tests. As illustrated above, it is affected by the prevalence in the samples of the tests. And, even given two tests, with sample prevalence 50%, suppose test A has a sensitivity of 100%, but specificity 0%, and test B has a sensitivity of 0% and specificity 100%. Both tests give the same probability of a correct result, yet the two tests are radically different.
The measures of the accuracy of a diagnostic test are sensitivity and specificity. The accuracy statistic, the probability of a correct test result, is not a measure of the intrinsic accuracy of a test.
For more information, see our online documentation:
Measures of diagnostic accuracy
Comments
Comments are now closed.